不等式を理解するのは、意外と簡単です。
数学が苦手な人でも、ちょっとしたコツを押さえれば、短時間で解けるようになります。
今回は、5分で不等式の解法をマスターすることを目指して、ポイントを絞って解説します。
数式の「大きい」「小さい」を理解して、解法のコツをつかみましょう。5分でスラスラ解けるようになるので、ぜひチャレンジしてみてください!
- 不等号の意味と種類
- 不等式の基本的な性質
- 不等式の解法

理解を深めるための練習問題も用意しているので、ぜひ挑戦してみてね!
不等号とは?
数学において、「不等式」とは、2つの数量の大小関係を表す式のことです。
具体的には、ある数が他の数より大きいか小さいか、またはそれと等しいかもしれないということを、記号を使って表現します。
このときに使われる記号が、いわゆる不等号と呼ばれるもので、以下のような種類があります。
| 記号 | 読み方 | 意味 |
|---|---|---|
| \(<\) | 小なり | 左が右より小さい |
| \(≦\) | 以下 | 左が右より小さい、または等しい |
| \(>\) | 大なり | 左が右より大きい |
| \(≧\) | 以上 | 左が右より大きい、または等しい |

不等式は不等号という記号が使われた方程式だよ!
具体例を使った理解:\(a<b,b>a\)の関係
たとえば、ある2つの数 a = 3、b = 5 とします。このとき、
\(a<b は 3<5\)
これは明らかに成り立ちます。この不等式を逆の向きで表すと、
\(b>a つまり 5>3\)
こちらも、もちろん正しいです。このように、不等式は向きを変えるときに不等号の向きも変える必要があります。つまり、
\(a<b⟺b>a\)
というように、意味は同じでも向きが逆になるのが大きな特徴です。
具体例を使った理解:\(a≦b,b≧a\)の関係
次に、\(a≦b\)という不等式を考えましょう。これは、「\(aは bより小さいか、aとbが等しい\)」という2つの可能性を含んでいます。
たとえば、
- \(a=4,b=4のとき、a ≦ b(つまり4≦4)は成り立つ(等しいから)。\)
- \(a=2,b=5のときも、2≦5なので成り立つ(小さいから)。\)
これを逆の立場で見てみると、「\(bはaより大きいか、等しい\)」と言い換えられます。つまり、
\(a≦b⟺b≧a\)
というふうに、不等号の向きが逆になっても、意味はまったく同じです。
不等式の解法
不等式の解法とは、xなどの文字が含まれる不等式を、数直線上でその値の範囲(解)として表すことをいいます。方程式と異なり、「等しい値」ではなく「範囲」で答える点が大きな特徴です。
- 性質①:両辺に同じ数を足しても不等式は変わらない。
- 性質②:両辺に正の数をかけても(割っても)不等式は変わらない。
- 性質③:両辺に負の数をかけたり割ったりすると不等号の向きが逆になる。
次の不等式を解きなさい。
\(−2x+5>11\)
この不等式を解くには、方程式と同じように移項や割り算を使って、xについて整理します。ただし、途中で負の数で割るときは不等号の向きが変わることに注意します。
\(−2x+5>11\)
\(−2x>11−5\) ① 定数項を移項する
\(−2x>6\) ② 両辺を -2 で割る(負の数なので不等号の向きを逆にする)
\(x<−3\)
解答:\(x<−3\)

不等式は値ではなく範囲で答えるよ!
不等式の解を数直線で表す
このような「範囲としての解」は、数直線上に図で表すと、とてもわかりやすくなります。
例
\(x<3\)
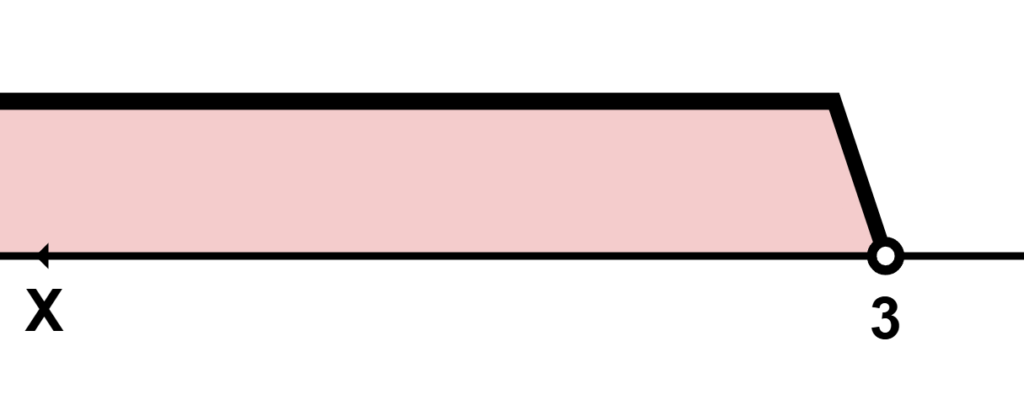

x<3を数直線上で表すとこんな感じ!
練習問題(解説付き)
次の不等式を解きなさい。
① \(3x+2<11\)
② \(−4x+1≧9\)
③ \(\dfrac{1}{2}x+3>\dfrac{3}{4}x+1\)
④ \(\dfrac{2x+5}{3}≦\dfrac{x-1}{2}\)

練習問題を用意したよ!それぞれの問題に答えと解説もついているから、自分の理解をチェックしてみてね!
【回答】※解説付き
① 問:\(3x+2<11\) 答え:\(x<3\)
解説:
\(3x<11−2⇒3x<9\) ① 定数項を移項する
\(x<3\) ② 両辺を3で割る
② 問:\(−4x+1≧9\) 答え:\(x≤−2\)
解説:
\(−4x≥9−1⇒−4x≥8\) ① 定数項を移項
\(x≤−2\) ② 両辺を-4で割る
③ 問:\(\dfrac{1}{2}x+3>\dfrac{3}{4}x+1\) 答え:\(x<8\)
解説:
\(3>\dfrac{3}{4}x-\dfrac{1}{2}x+1⇒3>\biggl(\dfrac{3}{4}-\dfrac{2}{4}\biggl)x+1⇒3>\dfrac{1}{4}x+1>\) ① 両辺から\(\frac{1}{2}x\)を引く
\(3−1>\dfrac{1}{4}x⇒2>\dfrac{1}{4}x\) ② 定数項を移項
\(8>x⇒x<8\) ③ 両辺を4倍
④ 問:\(\dfrac{2x+5}{3}≦\dfrac{x-1}{2}\) 答え:\(x≦−13\)
解説:
\(6⋅\dfrac{2x+5}{3}≦6⋅\dfrac{x-1}{2}⇒2(2x+5)≦3(x−1)\) ① 両辺の分母を払う(両辺に6をかける)
\(4x+10≦3x−3\) ② 分配して整理
\(4x−3x≦−3−10⇒x≦−13\) ③ 文字を左に、数を右に集める
まとめ
今回は、不等式の解法について、たった5分で理解できるようにポイントを絞って解説しました。以下のポイントを押さえることで、今後の数学の学習がぐっと楽になりますよ!
- 不等号の意味をしっかり理解することが基本です。小なり(<)、大なり(>)、以下(≤)、以上(≥)の記号の意味を把握しましょう。
- 不等式の解法では、移項や両辺に足したりかけたりする操作を使います。負の数で割るときは、不等号の向きが逆になることを忘れずに!
- 数直線で解を表すことで、解の範囲を視覚的に理解できます。不等式の解は「一つの値」ではなく、範囲として考えることが大切です。

これらをしっかり理解すれば、不等式を解く力がどんどん身についていきます。さらに練習問題を解くことで、知識が定着するので、積極的に挑戦してみてくださいね!



コメント